En la figura 4.2 se puede apreciar la analogía entre las neuronas biológicas y las redes neuronales artificiales. La red neuronal está compuesta por capas de nodos o neuronas artificiales, representados en la figura por círculos. La primera capa, conocida como capa de entrada.
Luego, la información pasa a través de una o más capas ocultas, cuya función es procesar y transformar los datos de manera no lineal, permitiendo que la red capture patrones más complejos.
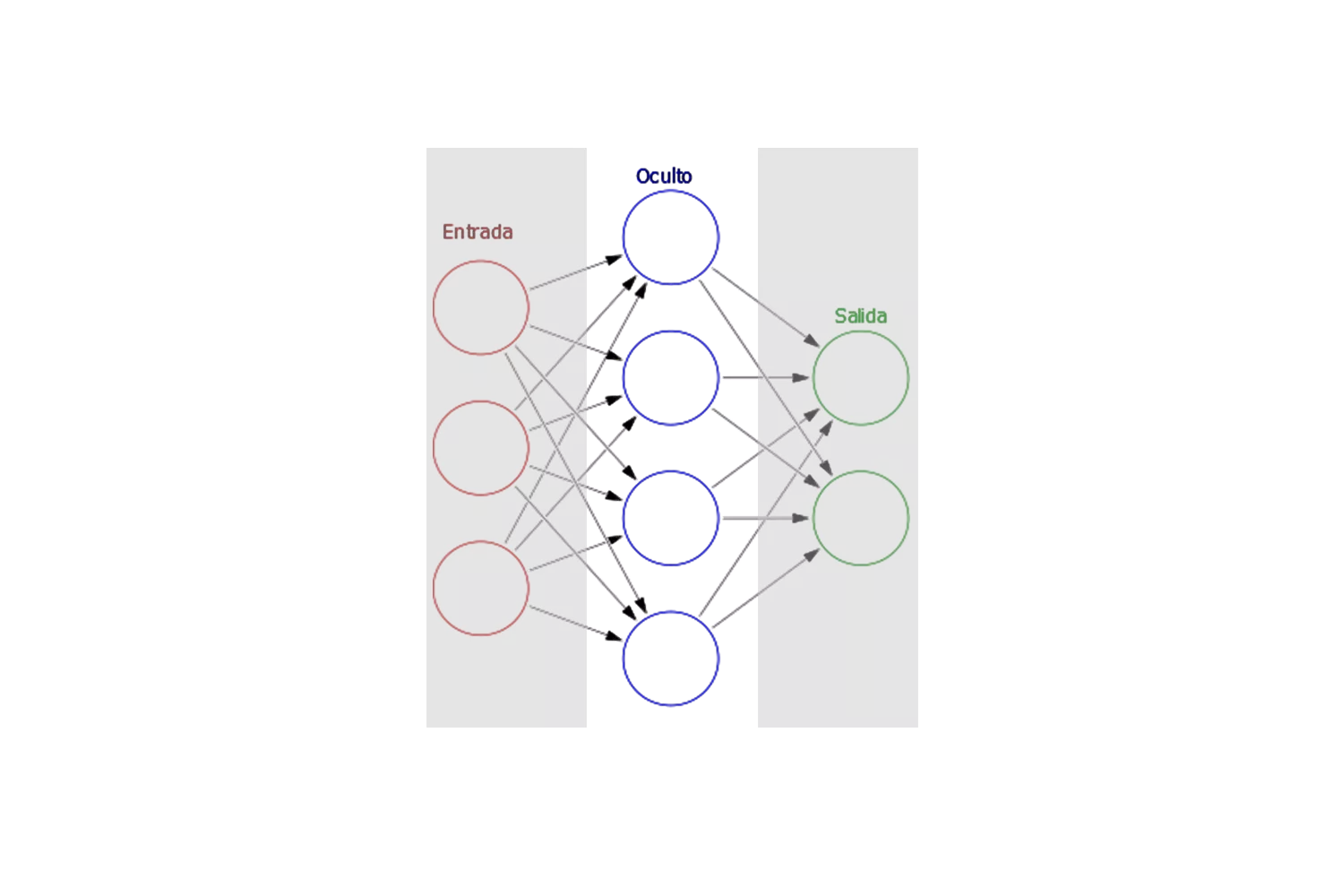
Finalmente, la información llega a la capa de salida, encargada de generar el resultado final o la predicción de la red.
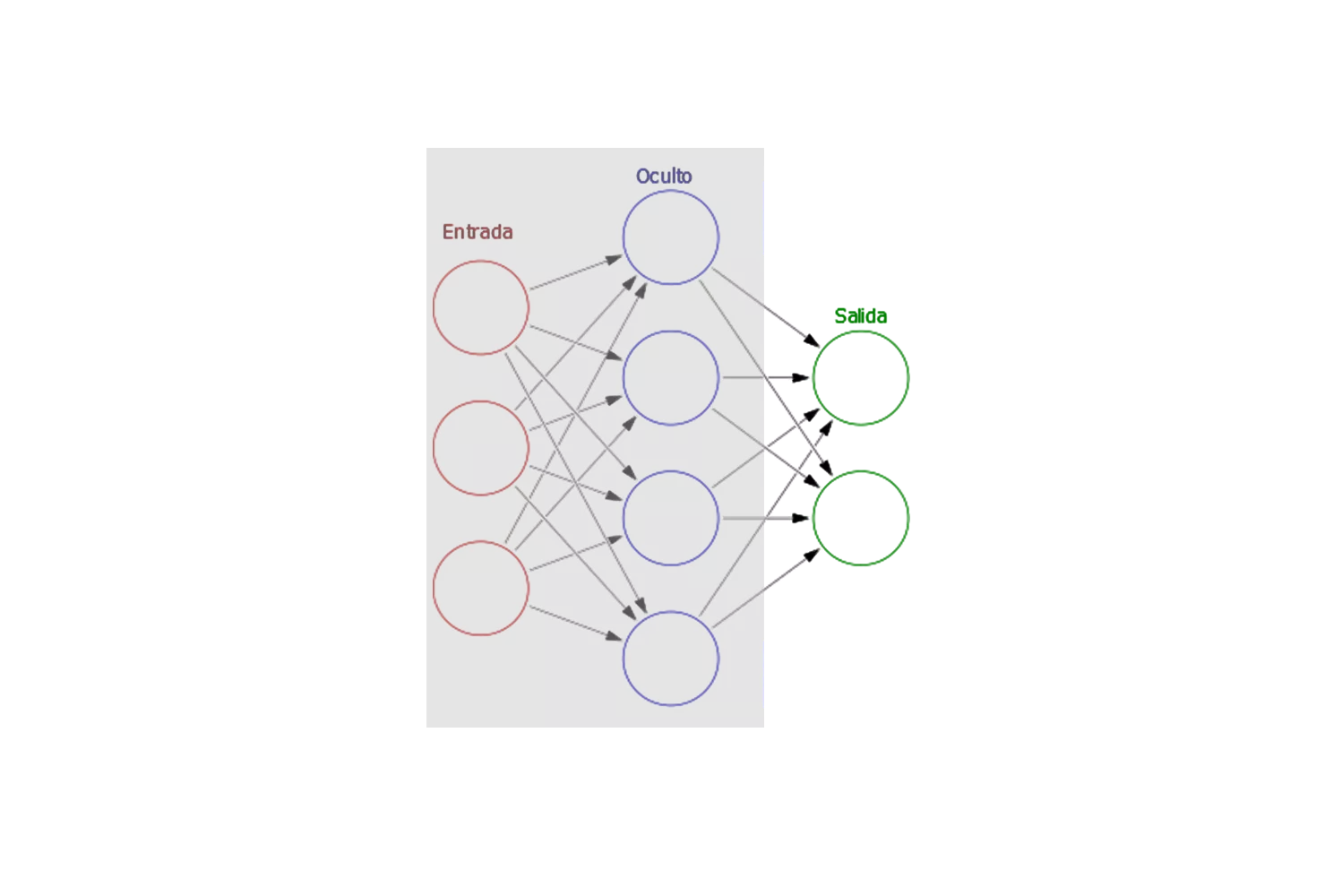
Cada una de estas capas está interconectada mediante Pesos, que determinan la importancia de las entradas que recibe cada neurona. A lo largo del entrenamiento de la red, estos pesos se ajustan para mejorar la precisión del modelo, permitiendo que la red aprenda de los datos y mejore su rendimiento en las tareas específicas para las que ha sido diseñada.
Otro elemento importante dentro de las redes neuronales, son las funciones de activación, que son funciones matemáticas que determinan la salida de un nodo basada en sus entradas.
Esta estructura de capas es fundamental para el funcionamiento de las redes neuronales, ya que permite la transformación progresiva de la información, desde las características más simples en la capa de entrada hasta patrones complejos en las capas ocultas, y finalmente una predicción precisa en la capa de salida.
Otros conceptos importantes relacionados con el entrenamiento de las redes neuronales son.
La retropropagación es un algoritmo fundamental utilizado en redes neuronales para optimizar los pesos de las conexiones entre los nodos. Su objetivo es reducir el error de predicción de la red ajustando los pesos de manera que la salida predicha se acerque lo más posible a la salida deseada.
El proceso de retropropagación se realiza en dos fases:
Fase hacia adelante (Forward Propagation):
Primero, los datos de entrada se procesan pasando a través de las capas de la red neuronal, aplicando activaciones en cada nodo, hasta obtener la salida final.
Fase hacia atrás (Backpropagation):
Luego, el error se propaga hacia atrás a través de la red, es decir, desde la capa de salida hasta las capas ocultas. Durante este proceso, se calcula el gradiente del error con respecto a los pesos usando la regla de la cadena del cálculo diferencial, y estos gradientes se usan para ajustar los pesos de cada conexión para minimizar el error.
La retropropagación se repite iterativamente hasta que el error se minimiza y la red puede hacer predicciones precisas.
La propagación hacia adelante es el paso inicial para procesar datos en una red neuronal y generar una salida.
Pasos del Proceso:
Este proceso se denomina “hacia adelante” porque los datos viajan de la capa de entrada hacia la capa de salida sin que se modifiquen durante el paso.
La optimización iterativa se refiere al proceso mediante el cual los parámetros de una red neuronal (principalmente los pesos y los sesgos) se ajustan de forma iterativa para minimizar una función de error. Este proceso es la base de muchos algoritmos de optimización que se utilizan en redes neuronales.
El algoritmo más común para la optimización iterativa es el Gradiente Descendente (GD), que realiza lo siguiente:
La optimización iterativa se refiere al proceso mediante el cual los parámetros de una red neuronal (principalmente los pesos y los sesgos) se ajustan de forma iterativa para minimizar una función de error. Este proceso es la base de muchos algoritmos de optimización que se utilizan en redes neuronales.
El algoritmo más común para la optimización iterativa es el Gradiente Descendente (GD), que realiza lo siguiente:
La optimización iterativa es un proceso clave en el entrenamiento de redes neuronales, que permite ajustar los parámetros (pesos y sesgos) para minimizar la función de error. Existen varias técnicas comunes y avanzadas que facilitan este proceso:
Utiliza un solo ejemplo de entrenamiento a la vez para actualizar los parámetros.
Divide el conjunto de datos en pequeños lotes (mini-batches) y utiliza un lote de ejemplos para actualizar los parámetros en cada iteración. Esto combina lo mejor de SGD y el Gradiente Descendente por Lotes.
Existen variantes como Adam, RMSprop, Adagrad, que ajustan dinámicamente la tasa de aprendizaje durante el entrenamiento, acelerando la convergencia y mejorando el rendimiento del modelo.
Cada uno de estos procesos es esencial para entrenar redes neuronales eficientemente y lograr buenos resultados en tareas de predicción y clasificación.
Para poder explicar el funcionamiento de una red neuronal de manera simplificada, vamos a extraer una sola capa de la red neuronal. A esta red neuronal simple de capa única (single layer neural network) la llamaremos Perceptrón simple.
Es la unidad básica de construcción de las redes neuronales artificiales complejas. Es fundamental para comprender las redes neuronales y es la entrada al mundo del Deep Learning.
Es la unidad básica de construcción de las redes neuronales artificiales complejas. Es fundamental para comprender las redes neuronales y es la entrada al mundo del Deep Learning.
Cada neurona de entrada representa una característica o atributo de los datos que estamos procesando. Por ejemplo, en un problema de clasificación de imágenes, cada neurona de entrada podría representar el valor de un píxel de la imagen. En la figura 4.3 estas neuronas de entrada están representadas con el vector Xi que tiene componentes.
A cada conexión entre las neuronas de entrada y la neurona de salida se le asigna un peso. Estos pesos determinan la importancia de cada entrada en la salida final. En la figura 4.3 los pesos se representan con el Vector Wi que tiene exactamente el mismo número de componentes que las entradas Xi:
El bias es un valor constante que se suma a la suma ponderada de las entradas. Actúa como un umbral que debe ser superado para que la neurona se active. Se representa con la letra B o con la letra griega β.
Esta función determina la salida de la neurona en función de la suma ponderada de las entradas y el bias. Las funciones de activación más comunes son la función escalón y la sigmoide. La función escalón se define de la siguiente manera:
Figura 4.3
Nota: Extraido de https://commons.wikimedia.org/wiki/File:Perceptr%C3%B3n.svg por Alejandro Cartas, 2015. bajo licencia de Creative Commons Attribution-Share Alike 4.0 International License.
De la figura 4.3 y después del análisis de los componentes se puede decir que la salida del Perceptrón simple se resume en la siguiente ecuación:
Cada neurona de entrada representa una característica o atributo de los datos que estamos procesando. Por ejemplo, en un problema de clasificación de imágenes, cada neurona de entrada podría representar el valor de un píxel de la imagen. En la figura 4.3 estas neuronas de entrada están representadas con el vector Xi que tiene componentes.
Inicializa los pesos sinápticos W. Los pesos W pueden ser iniciados con un valor aleatorio en un intervalo de [-1,1].
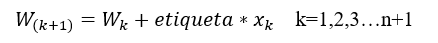
Si la salida del perceptrón es diferente a la clasificación deseada, actualiza los pesos sinápticos:
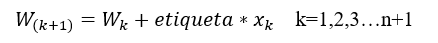
Nota: en caso que no sea un dataset separable, se puede condicionar la repetición a un número fijo de vueltas. Digamos 1000 veces.
Recursos: 0 Descargables
Duración: 1 Hora
Departamento de Sistemas e Informatica
sistemas@itistmo.edu.mx
“Por una tecnología propia como principio de libertad®️”