
Para empezar quiero que te fijes en el laberinto de la figura 3.3. Ahora, imagina que cada posición dentro del laberinto es un estado y para encontrar la salida, debemos realizar una búsqueda a través de todos los posibles estados.
Para poder hacer eso, se necesita hacer un proceso de modelado, donde podamos expresar las características de los problemas usando un lenguaje formal común. Es aquí donde los espacios de estado juegan un papel relevante, puesto que son una forma de representar o modelar problemas y sus posibles mecanismos de solución.
En definitiva un espacio de estados es una representación gráfica de un problema donde cada nodo en este grafo representa un posible estado del problema, y las aristas representan las acciones que pueden transformar un estado en otro. Un ejemplo de representación de espacio de estados es el que nos muestra la figura 3.4. donde cada nodo representa un estado y cada arista la acción a realizar.
En la misma figura 3.3 podemos ver algunos elementos que no he mencionado, por lo que para interpretar la información veamos cuáles son los componentes de un espacio de estados:
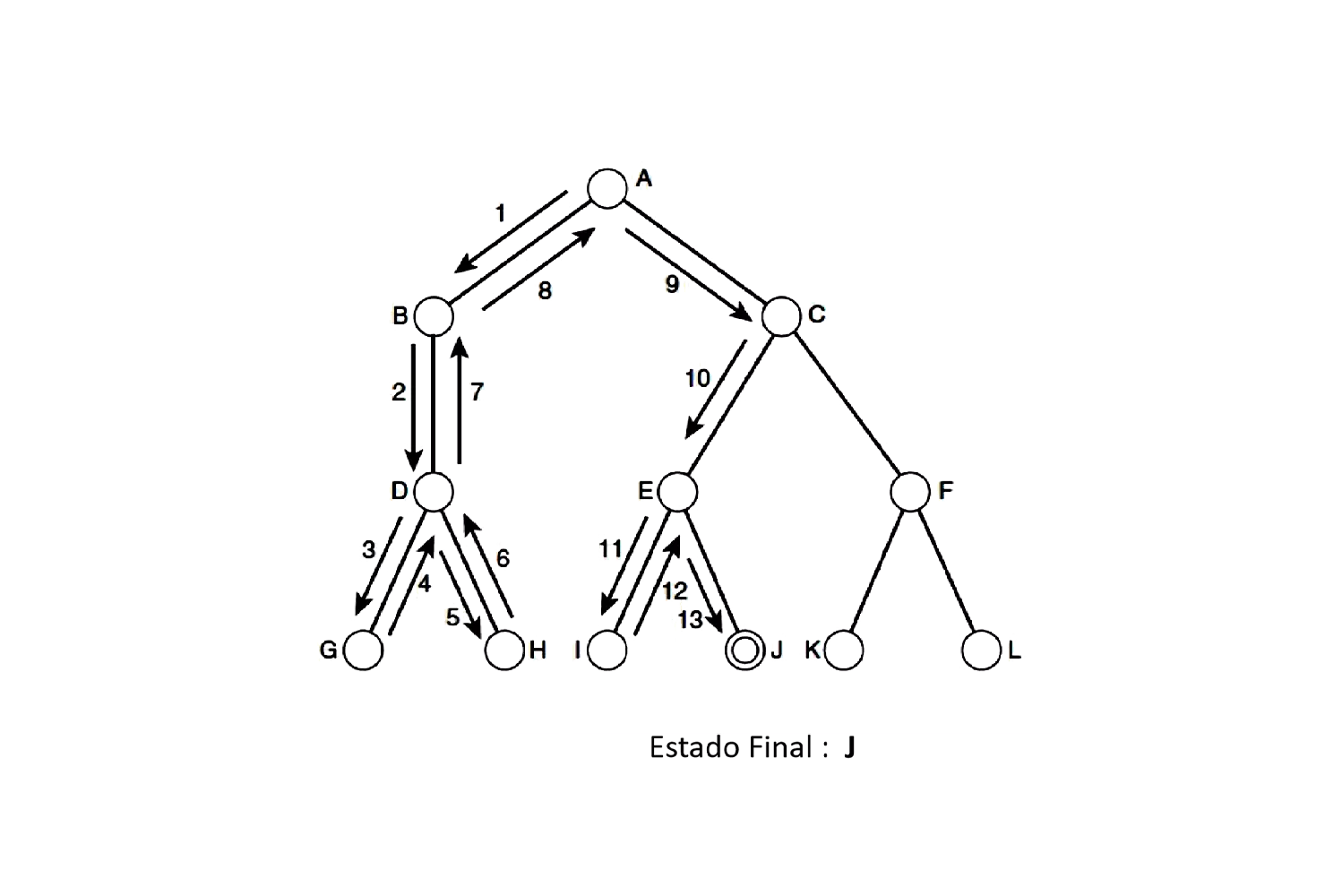
Representan todas las posibles configuraciones del problema, en la figura se muestran como nodos representados en círculos.
Son las reglas o movimientos que permiten la transición entre estados. Se encuentran descritos encima de las aristas entre nodos. Por ejemplo “avanza hacia arriba” o “avanza hacia la izquierda”.
El punto de partida. Cada problema debe tener un punto de inicio y ese punto es el estado inicial.
La solución o conjunto de soluciones del problema.
Los espacios de estados se pueden pueden dividir en dos tipos. Los determinísticos y los no determinísticos.
Es aquel en el que cada acción o operador aplicado a un estado lleva a un único estado sucesor predecible.
En otras palabras, no hay ambigüedad sobre qué sucederá cuando se aplique una acción. La figura 3.4 es un ejemplo de un espacio de estados determinístico.
Característica clave:
Ejemplo:
Estados:
Posiciones del robot en la cuadrícula.
Operadores:
Estado inicial:
Estado meta:
Figura 3.5
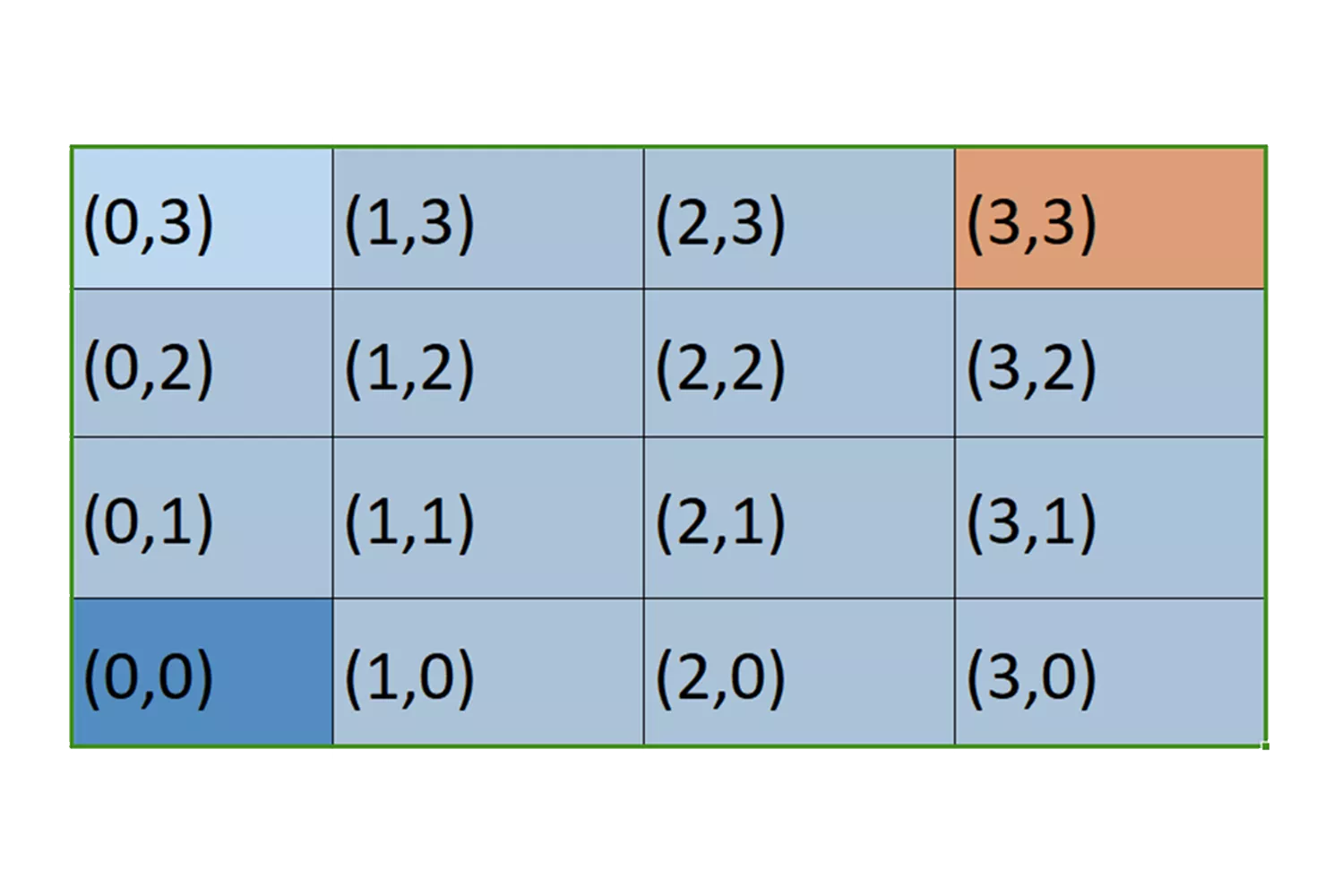
Nota: Cada casilla representa un estado y cada estado es una posición (x,y) en el tablero.
En la figura 3.5 se muestra el entorno donde se mueve el robot del ejemplo. Donde el estado inicial es la posición (0,0) y la meta es la posición(3,3).
Es aquel en el que la aplicación de una acción o regla puede resultar en varios posibles estados sucesores. Una misma acción en un mismo estado puede llevar a diferentes estados siguientes. Aquí, la acción aplicada no garantiza un resultado único, e introduce incertidumbre en el proceso.
Ejemplo:
Juegos como el póker, donde la acción de un jugador depende del azar o de las decisiones de otros jugadores.
Imaginemos el mismo robot de antes, pero ahora en un entorno donde algunos caminos pueden estar bloqueados de forma aleatoria. El robot puede intentar moverse, pero no siempre puede predecir si el camino estará libre o no.
Estados:
Posiciones del robot en la cuadrícula.
Operadores:
Estado inicial:
Estado meta:
| Característica | Determinístico | No Determinístico |
|---|---|---|
| Resultado de acciones | Un estado sucesor predecible | Múltiples estados sucesores posibles |
| Incertidumbre | No hay incertidumbre en las transiciones | La incertidumbre está presente en las transiciones |
| Ejemplo | Ajedrez, rompecabezas | Póker, sistemas donde hay aleatoriedad |
| Aplicaciones en IA | Juegos de estrategia, problemas de planificación | Juegos de azar, ambientes inciertos |
Tienes un robot que debe moverse en una cuadrícula de 4×4 desde la posición inicial (0,0) hasta la meta (3,3). El robot puede moverse en las cuatro direcciones: arriba, abajo, izquierda, derecha, y no hay obstáculos.
En la figura 3.5 se muestra el entorno donde se mueve el robot del ejemplo. Donde el estado inicial es la posición (0,0) y la meta es la posición(3,3).
Para resolver este problema, lo primero que debemos hacer es considerar los elementos que tenemos:
Posición inicial
(0,0)
Meta:
(3,3)
Acción:
Tienes un robot que debe moverse en una cuadrícula de 4×4 desde la posición inicial (0,0) hasta la meta (3,3). El robot puede moverse en las cuatro direcciones: arriba, abajo, izquierda, derecha, y no hay obstáculos.
Tomando en cuenta la figura 3.5, podemos hacernos una idea de los espacios de estados. Y para confirmar los movimientos vamos a representarlo gráficamente.
Figura 3.6
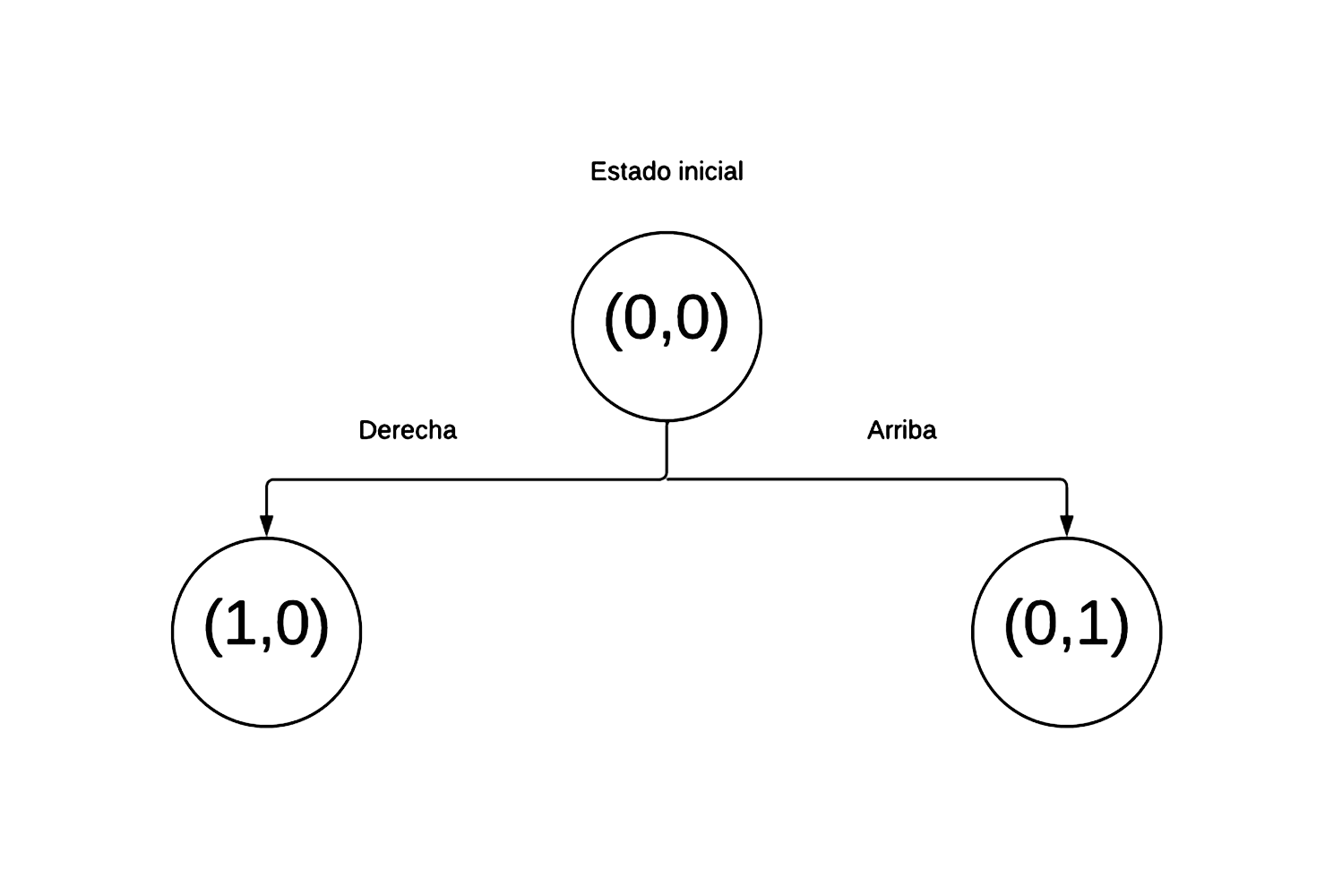
En la figura 3.6 podemos observar el primer nivel del diagrama que representa el espacio de estados. En ella, se pueden ver tanto el estado inicial como las primeras dos posibles acciones que se pueden hacer partiendo desde la posición (0,0). Si vamos a la derecha el siguiente estado es la posición en el tablero (1,0). Sin embargo si vamos hacia arriba el siguiente estado es la posición en el tablero (0,1).
Como se muestra en la figura 3.7, en este nivel se amplían las posibles acciones conforme la posición en el tablero lo permite. El árbol comienza a expandirse significativamente.
Figura 3.7
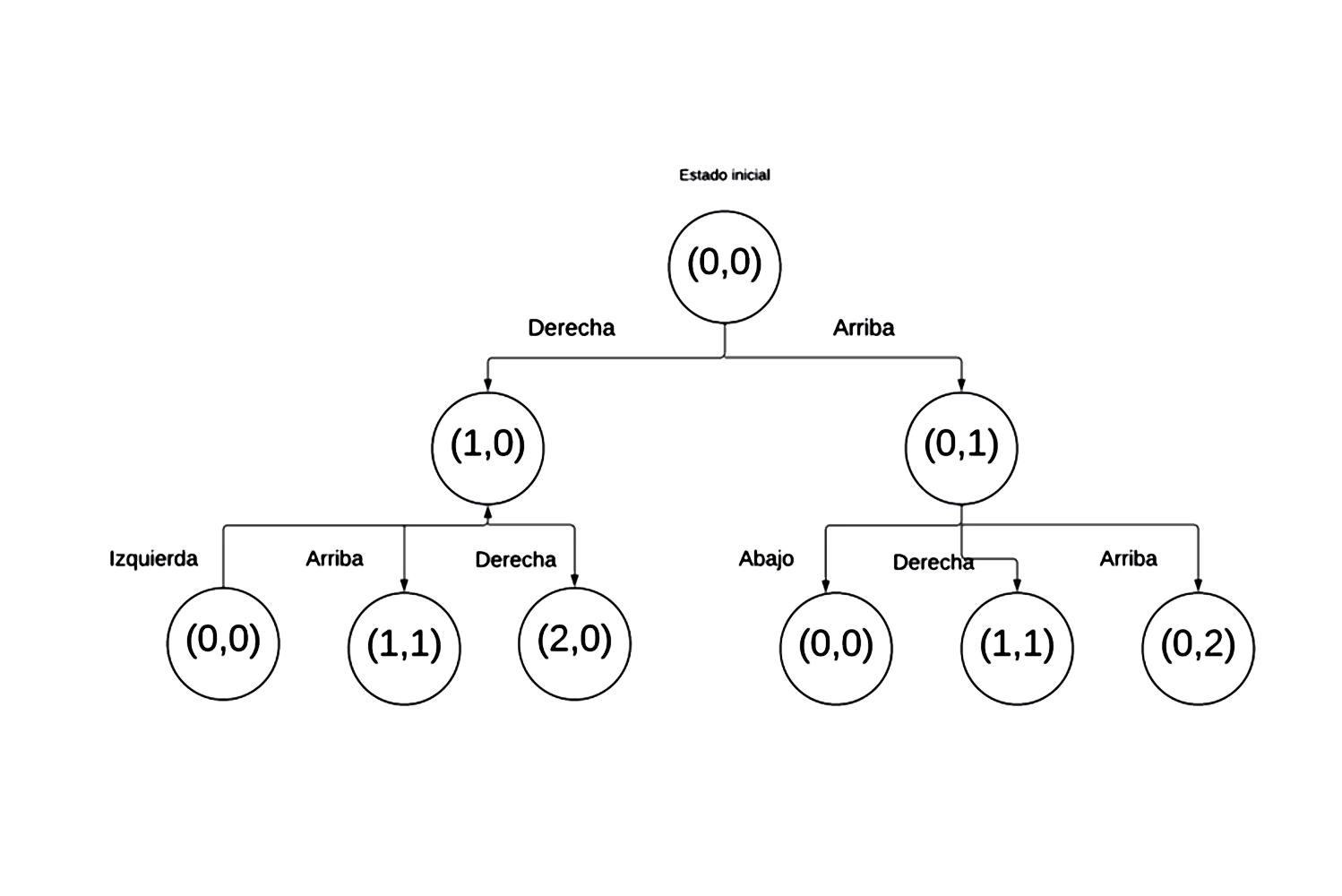
En este segundo nivel, vemos cómo se amplían las posibles acciones conforme la posición en el tablero lo permita. El árbol se va ampliando mucho, sin embargo intentaré ampliarla en la siguiente figura 3.8.
Como se muestra en la figura 3.7, en este nivel se amplían las posibles acciones conforme la posición en el tablero lo permite. El árbol comienza a expandirse significativamente.
Figura 3.8
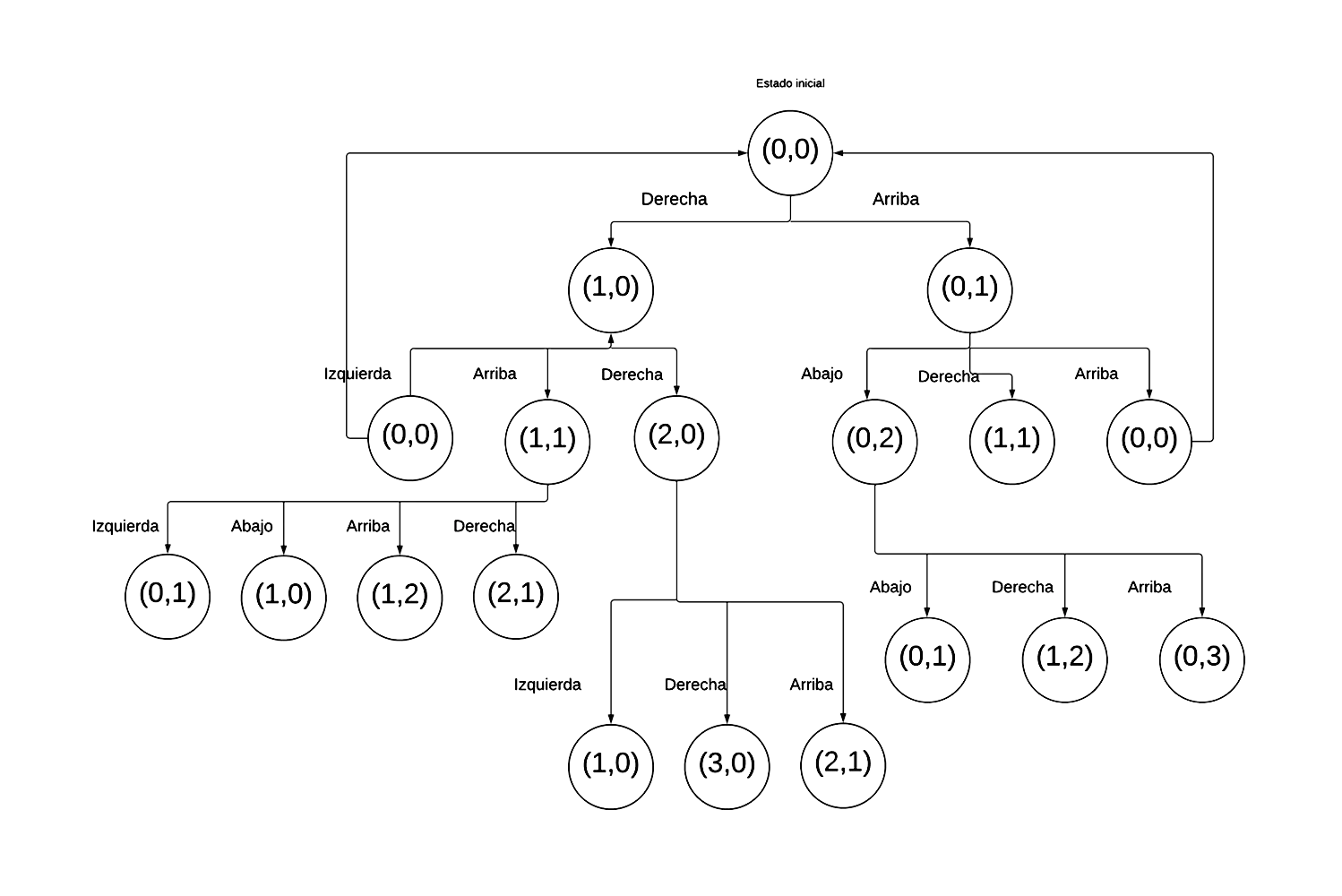
En este tercer nivel, algunos estados se repiten en diferentes ramificaciones del árbol. Como por ejemplo (0,0) o (1,1) y muchos otros se irán repitiendo a lo largo del desarrollo de toda la representación, porque el robot puede llegar a esos mismos estados desde diferentes estados o posiciones en el tablero. Si observamos bien la figura 3.5, veremos que la ruta más directa de acuerdo a los movimientos permitidos es la siguiente:
Ruta directa:
Pero también podemos llegar a la meta tomando otro camino:
Ruta alternativa:
El objetivo de esta representación gráfica es mostrar los distintos caminos que el robot puede tomar dependiendo del punto de partida y con esto ver todos los estados posibles que pueden ser activados. Todas esas posibilidades de movimientos y estados son lo que conforman un Espacio de Estados.
Problema del misionero y el caníbal con Espacios de estados. (INDIVIDUAL)

Descripción del Problema:
Imagina tres misioneros y tres caníbales que se encuentran en un lado de un río y desean cruzar al otro lado. Disponen de una barca que solo puede transportar a dos personas a la vez. El objetivo es que todos crucen el río sin que en ningún momento los caníbales superen en número a los misioneros en ninguna de las orillas (ni en la barca), ya que en ese caso los misioneros serían devorados.
Objetivo:
Instrucciones:
1. Modelado del Problema:
Estados:
Cada estado se representa como un vector (M, C, B), donde M es el número de misioneros en la orilla inicial, C es el número de caníbales en la orilla inicial y B indica si la barca está en la orilla inicial (0) o final (1).
Acciones:
Las posibles acciones son:
Restricciones:
Detalle de criterios:
Entregables:

Recursos: 1 Descargable
Duración: 2 Horas