Una pregunta que da inicio a la clase ¿Los seres humanos tomamos decisiones al azar?
Una vez guiado al alumno a darse cuenta que existen decisiones que tomamos sin la información completa, solo nos queda una cosa, razonamiento probabilístico.
El razonamiento probabilístico es un enfoque de la toma de decisiones y la inferencia que se basa en la teoría de la probabilidad. En lugar de depender únicamente de la lógica clásica, que se basa en premisas verdaderas o falsas, el razonamiento probabilístico permite manejar la incertidumbre al asignar probabilidades a diferentes eventos o conclusiones.
Por lo anterior es importante recordar el concepto de probabilidad:
Probabilidad:
Definición:
La probabilidad es la base del razonamiento probabilístico y se basa en:
Las conclusiones resultantes del razonamiento probabilístico, se derivan de la evaluación de la probabilidad de que ciertos eventos ocurran. Esto implica utilizar evidencia y datos disponibles para calcular la probabilidad de que una determinada hipótesis sea verdadera o falsa. Las conclusiones pueden ser más flexibles y estar sujetas a revisión a medida que se adquiere nueva información.
Para resolver problemas usando el razonamiento probabilístico se pueden usar diferentes teoremas de probabilidad. Entre ellos están:
Existen diferentes herramientas que nos permiten llegar a conclusiones basadas en probabilidad, estas son:
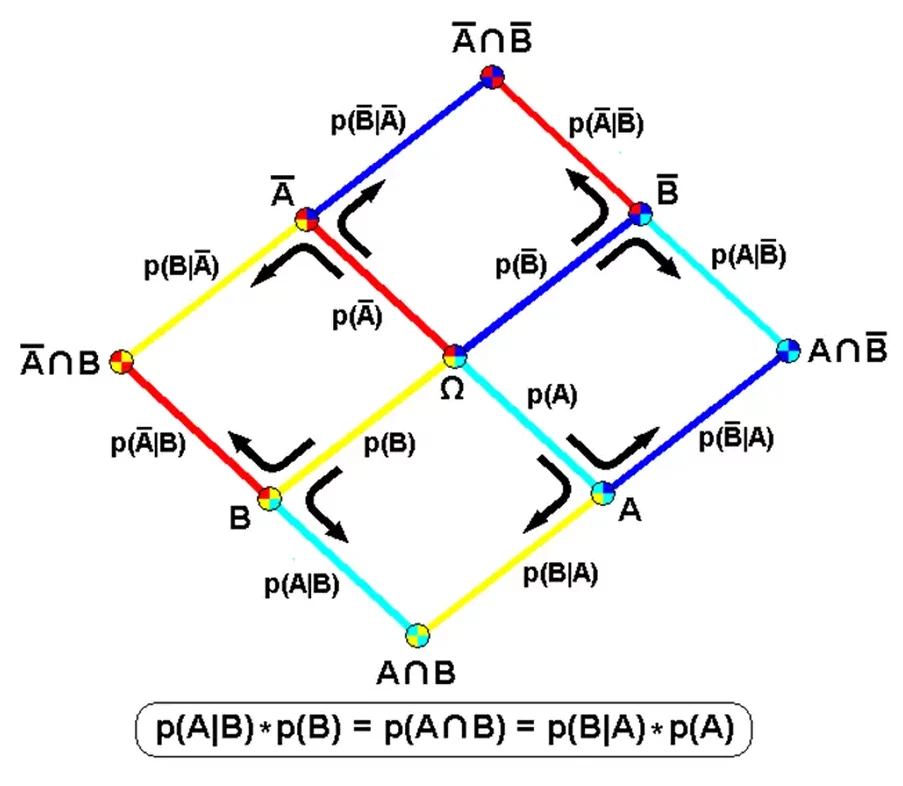
El razonamiento probabilístico se aplica en una amplia variedad de campos, incluyendo la inteligencia artificial, la estadística, la medicina, la ingeniería y la toma de decisiones en general. Al considerar la incertidumbre y la variabilidad inherente en muchos problemas del mundo real, el razonamiento probabilístico proporciona un marco sólido para modelar y abordar estas situaciones de manera más realista y efectiva.
Existen diferentes herramientas que nos permiten llegar a conclusiones basadas en probabilidad, estas son:
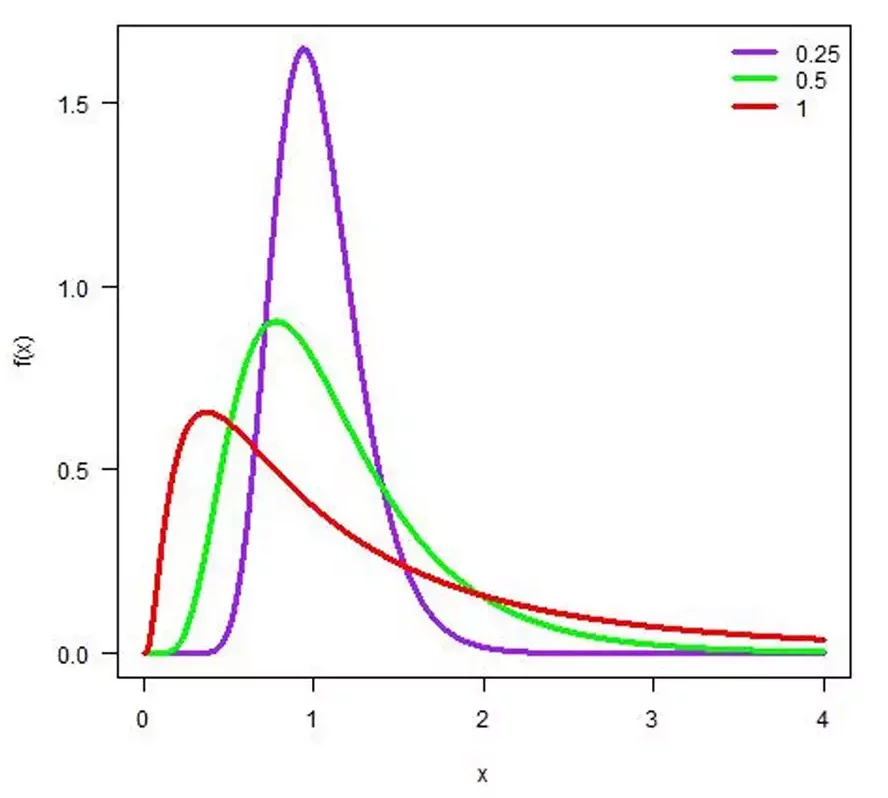
Pongamos que estás a punto de decidir dónde trabajar después de graduarse de la universidad. Tienes dos opciones: la primera ofrece un salario mucho más alto, pero implica mudarte a una ciudad diferente, lo que conlleva mayores gastos y estar separado de tu familia. Además, al ser un trabajo bien remunerado, hay una gran competencia por él. La segunda opción paga menos, pero lo suficiente para vivir en tu ciudad actual, con todas las ventajas que eso conlleva. Además, debido a la escasez de personas con tu perfil, tienes más probabilidades de ser aceptado.
¿Qué opción elegirías? Utiliza el teorema de sumas de probabilidades para justificar tu decisión.
Pros:
Contras:
Pros:
Contras:
Probabilidad de éxito si se trabaja en la ciudad diferente:
P(A) = P(ProsA) * P(no ContrasA)
P(A) = 0.9 * (1 - 0.8) * (1 - 0.9) * (1 - 0.6)
P(A) = 0.081
Probabilidad de éxito si se trabaja en tu ciudad:
P(B) = P(ProsB) * P(no ContrasB)
P(B) = 0.7 * (1 - 0.3) * (1 - 0.2) * (1 - 0.4)
P(B) = 0.42
Calcular la probabilidad total de éxito:
P(éxito) = P(A) + P(B)
P(éxito) = 0.081 + 0.42
P(éxito) = 0.501
Probabilidad de éxito al trabajar en la ciudad diferente:
P(A|éxito) = P(A) / P(éxito)
P(A|éxito) = 0.081 / 0.501
P(A|éxito) = 0.162
P(A|éxito) = 16.2%
Probabilidad de éxito al trabajar en tu ciudad:
P(B|éxito) = P(B) / P(éxito)
P(B|éxito) = 0.42 / 0.501
P(B|éxito) = 0.838
P(B|éxito) = 83.8%
En este caso, aunque la opción 1 ofrece un salario más alto, los gastos adicionales y la alta competencia pueden afectar significativamente la utilidad esperada. Por otro lado, la opción 2 puede ofrecer una mayor estabilidad y calidad de vida al evitar los gastos adicionales y tener una mayor probabilidad de ser aceptado. Con base a este análisis, la opción de trabajar en tu ciudad tiene una probabilidad de éxito mayor (83.8%) que la opción de trabajar en la ciudad diferente (16.2%).
En este ejemplo hemos usado un teorema muy básico del razonamiento probabilístico. En el siguiente subtema veremos el teorema de Bayes, que en aplicaciones reales y de inteligencia artificial es el más usado. El Teorema de Bayes ofrece un enfoque más sofisticado para actualizar y revisar nuestras creencias sobre un evento en función de la evidencia disponible, lo que lo convierte en una herramienta fundamental para la toma de decisiones.
Para este subtema se requiere contestar un cuestionario autoevaluable, el cual se encuentra en el apartado de recursos.
Cuestionario del subtema 2.7.
Recursos: 0 Descargables
Duración: 1 Hora
Departamento de Sistemas e Informatica
sistemas@itistmo.edu.mx
“Por una tecnología propia como principio de libertad®️”
